16984 Unique Cities

재밌게 푼 문제라 풀이를 적어봅니다. 풀이만 있는게 아니라 잡설도 좀 있을예정 ..

 

문제 요약 .. ? 은 귀찮으니 안하겠습니다 ㅋㅋ;;

 

 

 

 

제일 중요한 핵심은 이거라고 생각했습니다.

어떤 정점에 대해, 서브트리중 제일 깊은 서브트리를 제외하면 나머지 서브트리에서는 Unique City가 나올 수 없다

모든 방향의 Unique City를 계산하면 TLE가 나므로, 깊은 곳을 제외하면 탐색을 최대한 하지 않게 하는게 풀이의 핵심이라고 생각할 수 있습니다. 그래서 지름을 생각했습니다.

 

 

저 빨간 친구가 Unique City가 되는 정점들은, 저 빨간 정점의 서브트리 내부 외에는 존재할 수 없습니다. 그래서 서브트리 내부만 잘 계산해주는 느낌이라고 생각했는데,

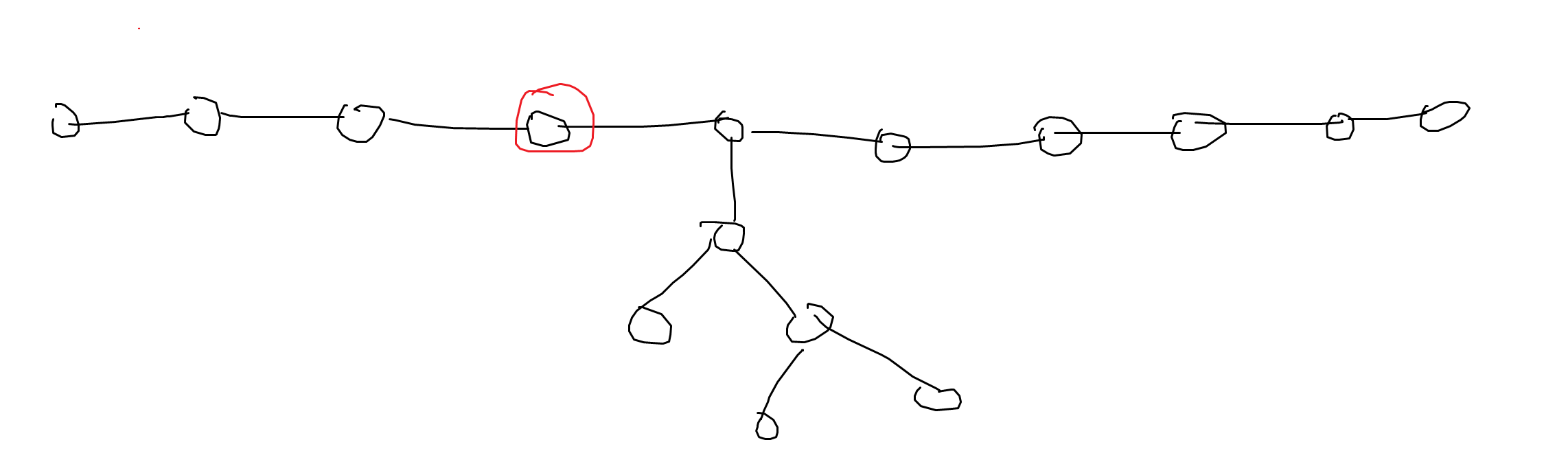
지름 위의 정점은 잘 처리해주기가 힘들었습니다. 저걸 계산하기 위해서는 또 따로 DFS를 돌아야하는지라 ..

 

그래서 다음과 같이 생각했습니다.

(맨 위의 줄이 지름입니다. 사실 저 트리에서는 엄밀히 따지면 지름이 아니긴 한데 ;; 지름이라고 생각합시다 ㅋㅋ)

 

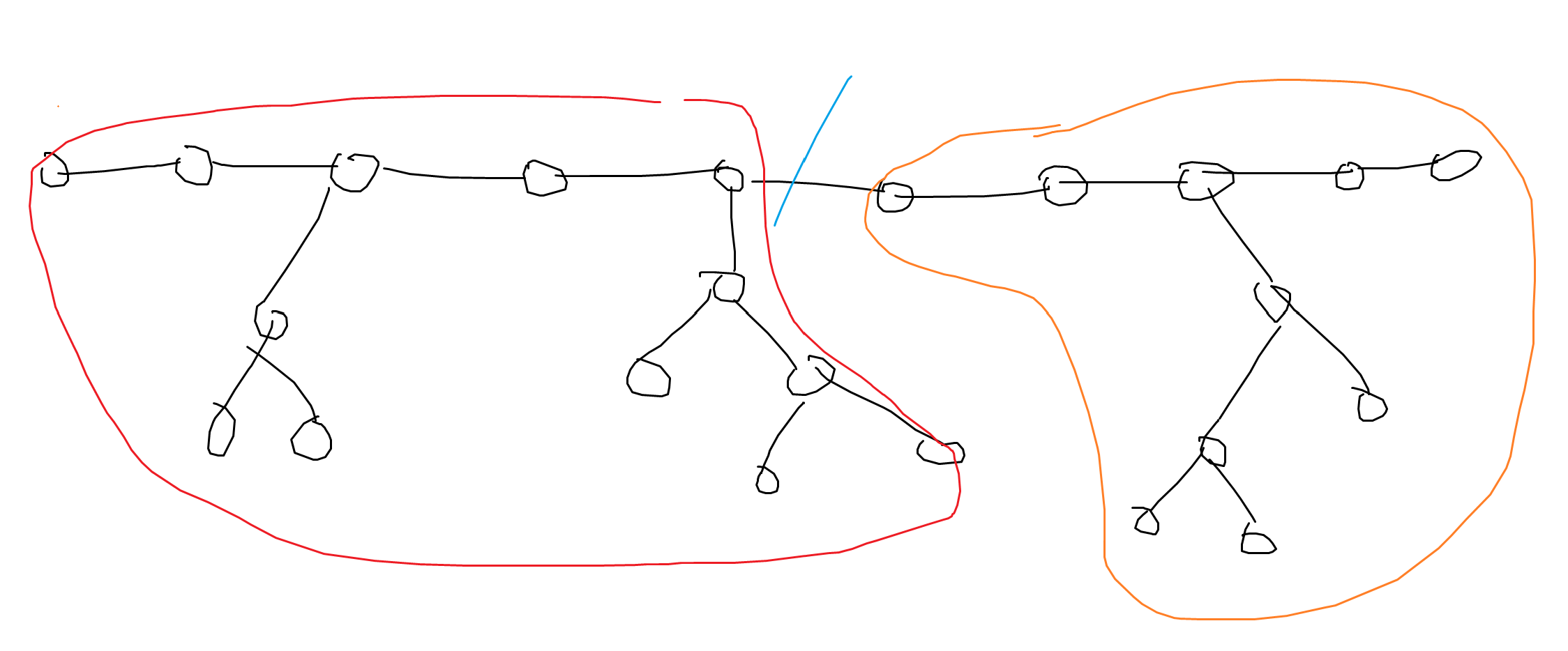
빨간 부분의 정점에 대해 답을 구한다고 하면, "깊이가 제일 깊은 서브트리"는 무조건 주황색 쪽으로 가는 서브트리입니다.

반대로 주황 부분에 대해서도 같은 논리가 성립합니다. 이를 이용해서, 세그로 스위핑을 하는 건줄 알았습니다. 지름 위의 애들에 대해서는, 

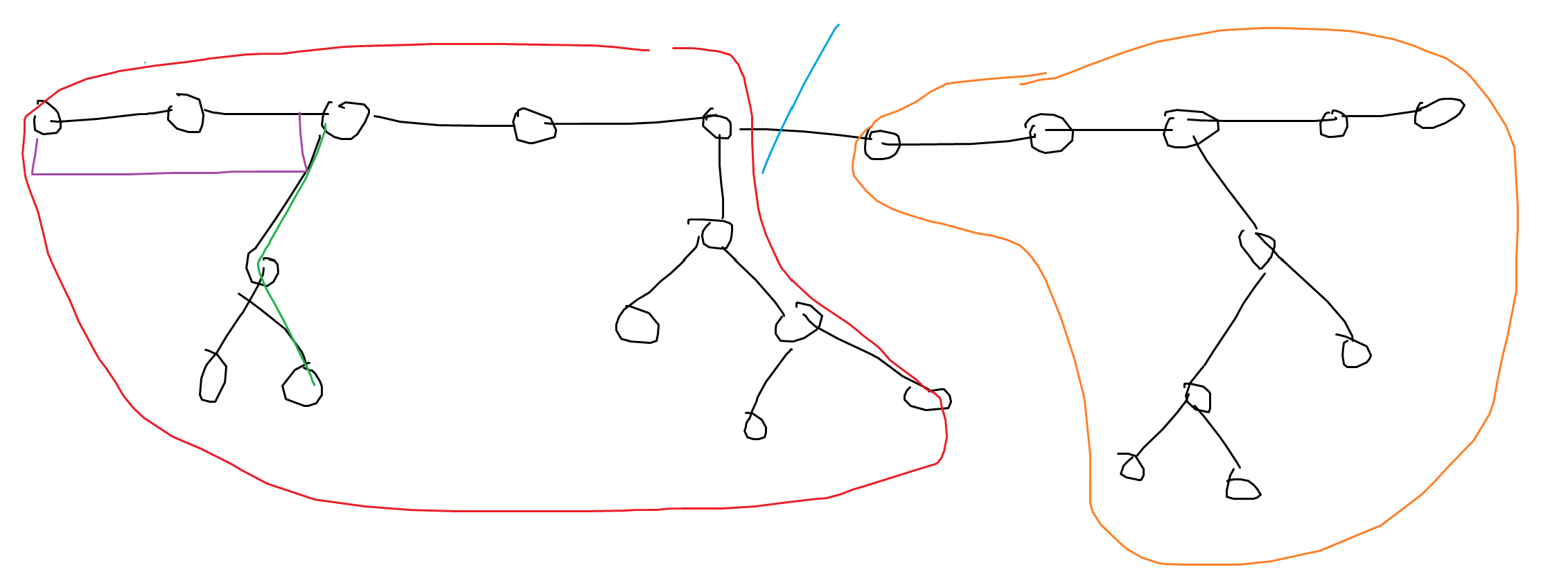
보라색 길이가 연두색 길이 (곁다리 서브트리의 깊이)보다 항상 같거나 크므로, "메인 스트림"은 항상 지름이 됩니다. 그래서 지름 위의 정점들을 관리하면서, 지름 위에서 하나씩 포인터를 움직일 때마다 곁다리 서브트리의 높이만큼 앞의 정점 몇개를 날려주면 됐습니다.

 

문제는 서브트리로 내려갈 때 발생합니다. 스위핑하면서 값을 재활용할 수 있을거라 생각했는데, 그게 잘 안 됐습니다.

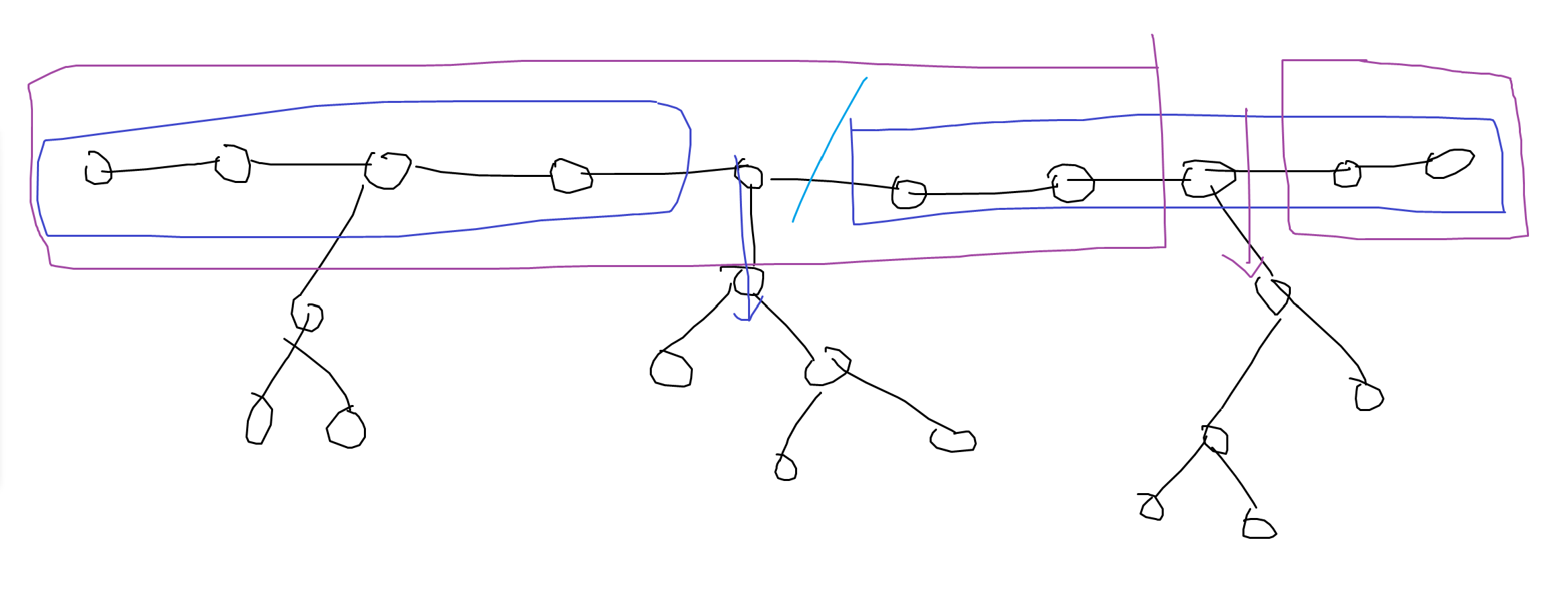
왼쪽에서부터 두번째 서브트리로 내려가기 위해서는 파란 구간들의 정보를 써야하고, 맨 오른쪽 섭트로 내려가기 위해서는 보라 구간의 정보가 필요합니다. 근데 저 구간을 서브트리로 내려가면서 훼손한다면, 그 다음 서브트리에서 그 정보를 쓰기가 힘듭니다. 다시 복원하는데 시복이 더 들기 때문입니다 ㅋㅋ.

 

그래서 이 풀이는 좀 짜친다고 생각하여, 아이디어만 가져온 다른 접근을 생각했습니다.

 

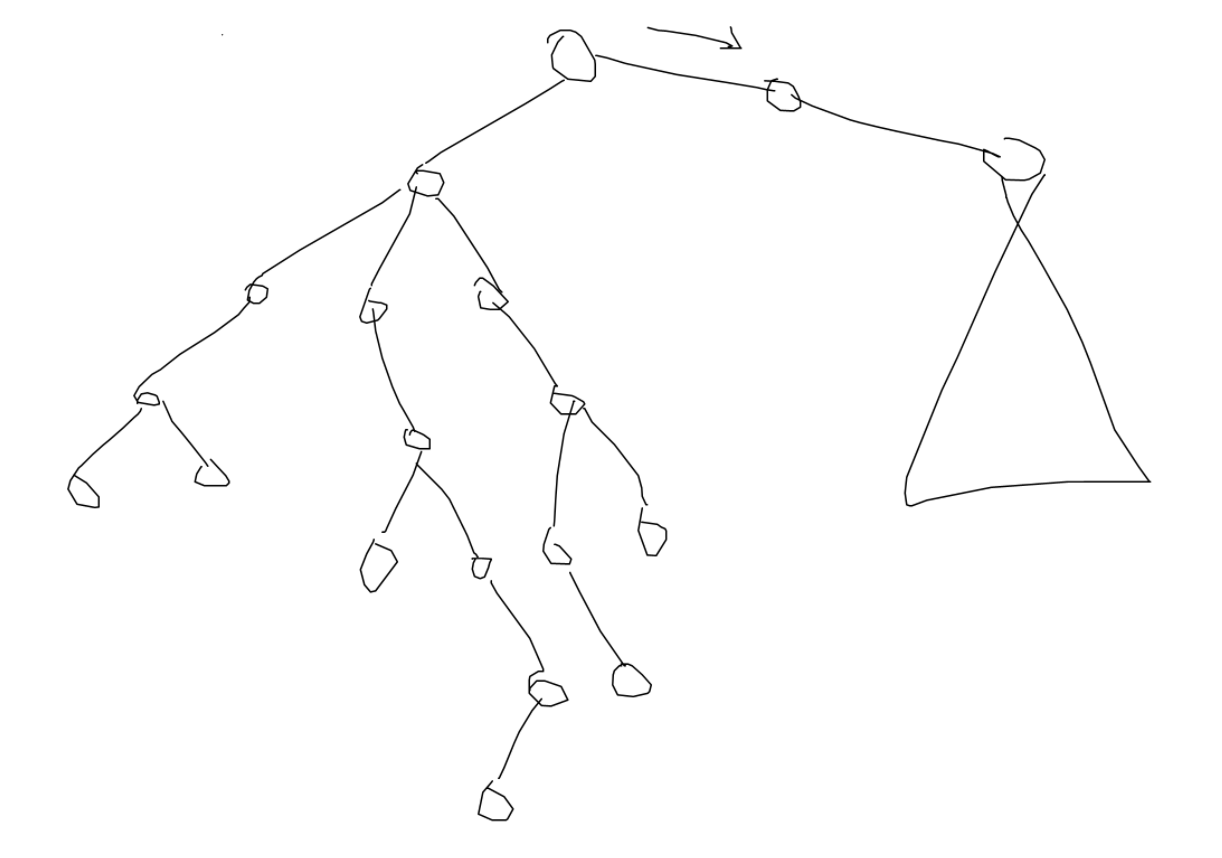
이런 트리가 있다고 생각해봅시다. 오른쪽 서브트리는 제일 깊은 정점이 있는 서브트리입니다. 만약 저쪽 서브트리가 아닌 반대쪽 서브트리의 값을 계산한다고 생각해봅시다. 그러면 제일 먼 정점 (제일 깊은 서브트리)는 항상 오른쪽 서브트리 방향이 되게 됩니다. 즉, 부모쪽으로 올라가는 방향이죠. 그러면 이제 오른쪽 서브트리의 정보와, 부모-자신을 잇는 경로의 도시들만 관리하면 됩니다. 그 외의 도시들은 어차피 Unique City가 될 수 없기 때문이죠.

저 빨간 경로상에 없다면, 오른쪽 서브트리의 (또는 빨간 경로상의) 어떤 정점 x가 존재해, 파란 정점 (답을 계산하려는 정점)과의 걸이가 같아지게 됩니다.

그래서 여기서 생각한 풀이는 오른쪽 서브트리의 정보를 스택으로 관리하고, 왼쪽 서브트리로 내려가면서 스택을 관리해주는 풀이였습니다. 아 물론 오른쪽 서브트리를 이후에 어떻게 처리할지는 생각 안했죠 ㅋㅋ;;

 

 

문제는 그 다음입니다. 많은 자식중에 어떤 한 자식으로 내려가기로 정했으면, 다른 자식쪽 서브트리의 깊이만큼 stack에서 pop을 해 줘야 합니다.

초록색 자식으로 내려가기로 했다면, 옆의 친척?쪽 서브트리의 정점들에 의해 기존에 Unique City였던 애들이 불가능해집니다. 정확히는 stack에서 몇개 pop이 됩니다.

여기서 조금 아이디어가 필요합니다. HLD 비슷하게 하는 겁니다.

자식들 중 제일 깊이가 깊은 서브트리 쪽으로 Heavy간선을 잇습니다.

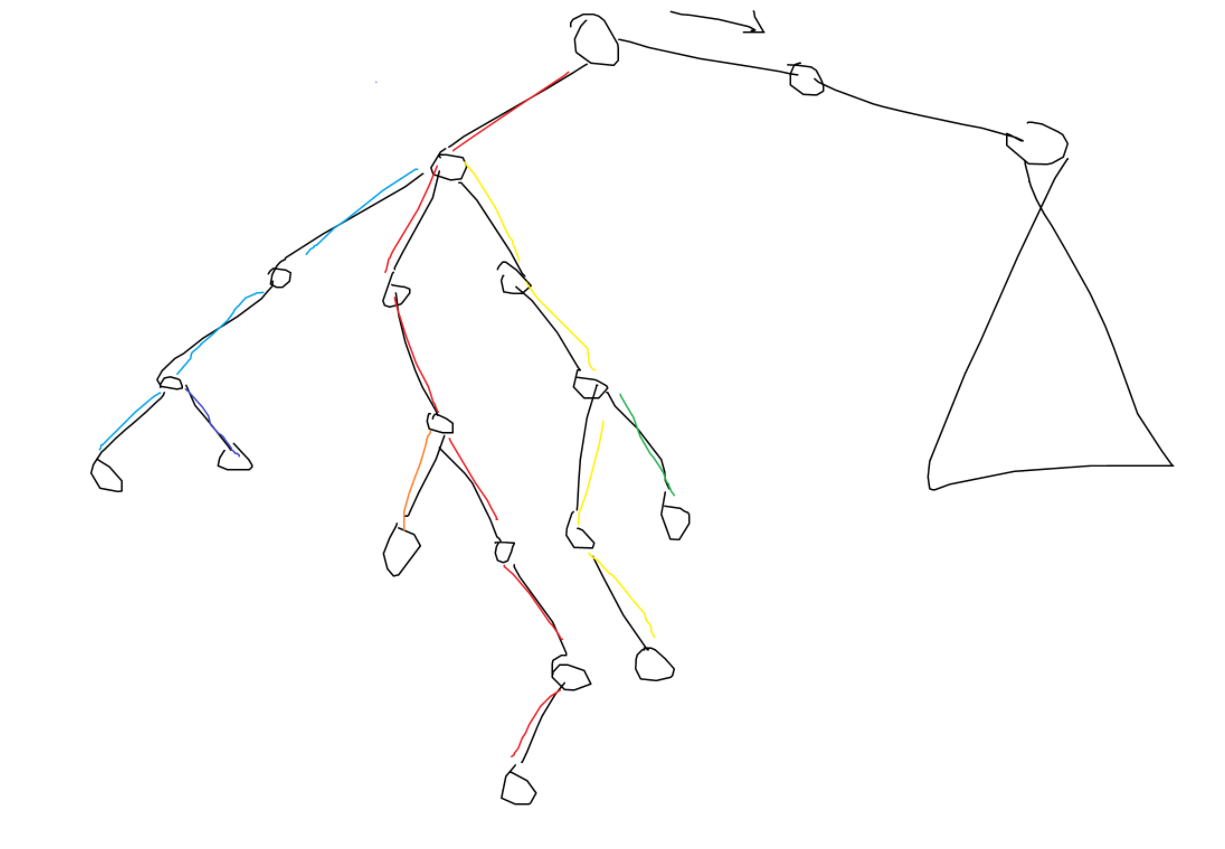
제일 먼저 Heavy쪽으로 쭉 내려갈 겁니다. 쭉 내려가면서, 곁다리 서브트리의 깊이만큼 stack에서 갱신을 해 줍니다.

리프에 도달하게 되면, 차례차례 올라가면서 답을 구해줄겁니다. DFS할 때 return하기 바로 전에 답을 구해주는 겁니다.

 

리프를 처리한다 생각해봅시다. stack은 이미 갱신이 다 되어있으므로, 바로 답을 낼 수 있습니다.

하나씩 올라가면서, 자기 아래쪽 서브트리의 깊이만큼 또 stack을 갱신해 줘야 합니다.

 

올라가다가, 옆의 곁다리 간선을 만났다고 합시다. 이 경우는 곁다리 간선을 방문합니다. 곁다리 간선을 방문할 때, 스택을 갱신할 필요는 없습니다. "제일 깊은 라인"에 의해서 stack에서 제거되는 경우만을 생각하면 되는데, 이는 이미 DFS에서 heavy line을 타고 올라오면서 갱신해주고 있기 때문입니다. 이후는 곁다리 간선으로 내려가서 그 내부에서 heavy 라인, 즉 재귀를 해주면 됩니다.

 

문제는 반대쪽을 처리하기가 좀 곤란하다는 것인데, 이는 위의 아이디어를 다시 사용할 수 있습니다.

반대쪽을 처리하는데 곤란한 이유는 하나입니다. "깊은 곳이 바뀔 수 있기 때문". 항상 부모쪽이 깊은 곳이라면 쉽게 처리할 수 있지만, 바뀔 수 있다면 말이 달라집니다. 여기서 지름을 생각합니다.

지름을 반띵 후, 각각 반반을 따로 계산해주면 됩니다. 각각 부분은 방금 전에 했던 것처럼 처리할 수 있습니다. 왜냐? 항상 깊은 곳이 부모 방향이기 때문입니다. 풀이는 이상입니다.