$+1$과 $-1$로 되어있는 길이 $N$의 수열이 주어집니다. 그리고 $Q$개의 구간쿼리가 들어옵니다.
구간쿼리 내용은
구간의 수를 앞에서부터 누적합할 때와 뒤에서부터 누적합할 때, 음수가 나오지 않도록 $-1$을 몇 개 제거할 수 있다. 최소 횟수를 구하시오.
풀이
앞, 뒤 누적합이 아닌 한쪽 방향만 고려해봅시다. 누적합 그래프를 그려보면, 음수가 되지 않을 조건은 그래프가 처음 시작점보다 아래로 내려가지 않는 것입니다.

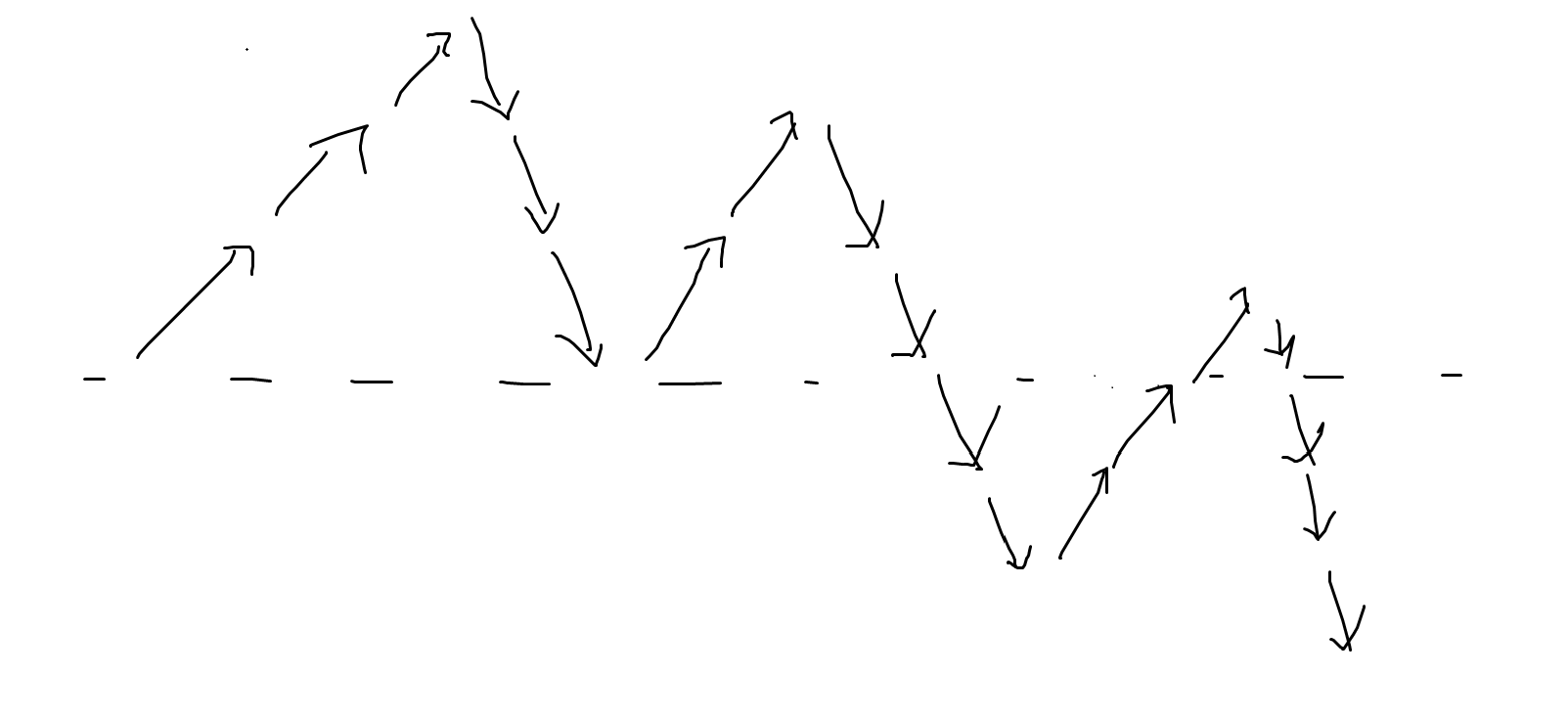
$-1$을 하나 없애는 것은, 그 이후의 값 전체에 $+1$, 즉 뒤를 들어올리는 것과 같은 연산이 됩니다. 최저점이 0 이상이 될 때까지 끌어올려야 하므로, 시작점, 즉 $l-1$에서의 누적합 최댓값 - $l~r$에서의 누적합 최솟값이 답이 됩니다.
이를 좀 다르게 접근할 수도 있습니다. 좀 더 엄밀한 접근이라고 해야하나?

$(b, d]$ 구간에서 $-1$을 하나 없애는 것은, $a - b$의 높이 차이를 상쇄해주지 못합니다. 그러므로 $a ~ b$구간에서 한번 시행을 써야 합니다. 또, $a ~ c$구간에서 한번 더 써줘야하고, $a ~ d$에서도 써 줘야 합니다. 이를 다음과 같이 사영하여

여러개의 구간으로 나타낼 수 있습니다. 이를 반대쪽에서도 적용해봅시다. 이 그래프를 그대로 들고가면, 반대로 이 경우는 시작점보다 값이 항상 낮게 있어야 합니다. 이 또한 구간으로 나타낼 수 있고,

각각 앞에서 볼때, 뒤에서 볼 때의 구간을 나타냅니다. 저 두 구간이 겹치는 곳에서 쓰면, 동시에 위아래를 제거할 수 있습니다. 즉, 최대한 많이 겹쳐서 쓰는게 주요 목표가 됩니다.
하지만 이렇게 보면 쉽지 않습니다. 각각에서 구간 자체가 많이 나올 경우, 겹치는 구간을 찾는데만 해도 시간이 걸릴 것입니다.
여기서 그리디 전략을 사용합니다. 한쪽은 계속 최대한 깊은 곳에 연산을 사용하는 겁니다.

위쪽 구간이 어떻든, 아래쪽 구간에서 항상 맨 끝에다가 연산을 하는 최적해가 존재합니다. 근데 다시 또 반대쪽 구간들을 보면 막막해집니다. 구간을 찾는거만 해도 걸리는데 구간당 매칭까지 해 줘야 합니다. $TLE$를 면하기 힘들어 보입니다.
하지만 다시 처음으로 돌아가봅시다. " 즉 $l-1$에서의 누적합 최댓값 - $l~r$에서의 누적합 최솟값이 답이 됩니다. ".
이를 뒤에서부터 볼 때도 적용하면, 누적합 배열이 적절히 갱신되었다는 전제 하에 쿼리 한번으로 처리할 수 있습니다.
이제 앞쪽에서 시작하는 구간을 처리해주는 일만 남았습니다. 연산을 사용할 때 누적합 배열이 변하는 것은 연산당 $O(logN)$에 레이지로 간단하게 처리할 수 있습니다. 문제는 해야 할 구간이 많다는 것이죠.
여기서 오프라인 쿼리를 생각해봅시다. 시작점이 같으면, 처리해야하는 구간의 형태도 동일합니다. 물론 $l~r$구간 외의 누적합 값에는 관련이 없으므로, 범위 밖으로 나가는 구간은 포함되지 않지만 이는 그리 중요하지 않습니다. 연산을 적용할 때 맨 끝에다가 적용하므로, 구간 밖으로 나가는 경우는 구간 내의 누적합을 건드리지 않습니다.
여기서 추가적인 간단한 관찰을 하면 오프라인 쿼리로 풀 수 있습니다.
위에서 구간을 구할 때 이를 트리로 나타낼 수 있습니다. 즉, $i$와 $i$이후의 $i$보다 누적합이 작아지는 지점을 간선으로 이으면, 이는 트리가 됩니다. 트리의 루트에서 $DFS$를 하면서, 한 번 내려갈 때마다 레이지 업데이트를 한 번 해주는 방식으로 전체 답을 구해줄 수 있습니다. 총 시간복잡도는 $O((N+Q)logN)$ 입니다.
'PS' 카테고리의 다른 글
| 개인적으로 출제한 문제 (0) | 2025.02.26 |
|---|---|
| 16984 Unique Cities (0) | 2025.01.25 |
| 21643 New Level (1) | 2025.01.04 |
| 18448 Best Subsequence (1) | 2025.01.04 |
| 17674 특별관광도시 (1) | 2025.01.04 |