음 망했나? 작년에는 근데 더 망한 관계로 비교적 잘 본거로 퉁치자.
끝나고 SCSC가 있는 관계로 5/17 하루 내내 서울대에 있었는데 개인적인 생각으로는 둘 다 적당히 상타치인 것 같아 기부니가 좋다.
일단 KMO가 먼저였다. 7시+-정도에 집을 나서서 7호선 타고 갔다.
9시 반까지 입실인데, 8시 반에 도착한 관계로 서울대 입구에 있는 편의점에서 급하게 삼김을 먹고 달렸다.
다행히도 빨리 도착할 수 있었고, 지인 NMK명을 만났다. 뽀구미라는 분을 만나고 싶었는데 그분이 지각한 관계로 못 봤다 ㅋㅋ
지금 후회하고 있는건 타임라인좀 적을걸
여기에 답이 나오는데, 그거 다 뇌피셜이다.
좀 찍은건 더더욱.
1번
작년 1번은 X쉬웠는데 그거만큼 쉽진 않아서 놀랐다. 그림을 그렸는데, 어 이거 값이 나오나?하고 좀 고민했다. 비율 2개 값이 각각은 안 일정한데 합이 일정한가? 하나를 1:1로 고정할까? 이런 뻘짓을 하다가 그냥 메넬 딸깍이란 걸 알고 풀었다.
근데 틀림. ㅋㅋㅋ 아니 왜 답이 14가 아님?
아마 답은 $34$이다.
2번
작년 2번보다 어려운 것 같다. 1번 조건에 의해 각 수가 모두 짝수거나 모두 홀수여야 한다. 2, 3번 조건 보면 그 두 경우마다 경우의 수가 똑같음을 알 수 있으므로. 하나만 구해서 $\times 2$하면 된다.
$mod 3$한 수열을 생각하면, 맨 앞에 2개를 정하면 그 다음부터는 유일하게 정해진다. 그러므로 $mod 3$ 수열을 정하는 경우가 $3 \times 3$가지, 그에 대응하는 원래 수열 개수 $2^8$가지, 그리고 마지막 곱하기 $2$를 하면 답이다.
$3^2 \times 2^8 \times 2 = 4068$
3번
$10!$부터는 $100$으로 나눈 나머지가 0이다. 나머진 그냥 열심히 계산했다. 답은 $13$
4번
식 정리하면 $|4x| <= |n|, 4 <= |4x-n|$이 나온다. $-1, 0, 1$만이 안되지만 $|n| <= 10$ 조건이 붙어있어 그냥 계산해도 답이 나올 것 같다. 답은 $21 - 3 = 18$.
5번
일단 답은 500이다. 아니 갑자기 5번 안풀림 이슈로 시간을 많이 날렸다 ㅋㅋ. 처음에 20분정도 보다가 나머지 문제가 혜자인 것 같아 6번부터 좀 풀고 다시 와서 풀었다. 참고로 원과 직선의 교점 구하는 이차방정식 풀어서 풀었다. ㅋㅋ
6번
르장드르 공식만 알면 풀 수 있다. Kummer로 비비는 고능한 풀이가 있는 것 같은데, 그건 잘 모르겠다. 걍 덩어리 묶어서 $[1/5] + [2/5] + [3/5] + \dots$ 계산하는걸 했다. 솔직히 $O(logN)$이라 얼마 걸리진 않는데, 곱셈 $N$번하느라 실수가 날 가능성이 크다. 다행히도 안 났다.
답은 $688$이다.
고능한 풀이로는 $250(1 - 1/5 + 1 - 1/25 + 1 - 1/125)$가 있는 듯 하다. 왜 되는진 몰루 그냥 식만 들었다.
7번
가능한 $(x^2+xy, xy+y^2)$ 쌍이 몇 개 없다.
$3, 4, 5 .. \dots 24$를 노드로 가지고 저 쌍마다 엣지가 존재하는 그래프를 생각하면, 각 연결 컴포넌트마다 하나를 정하면 나머지도 유일하게 정해진다. naive하게 컴포넌트 개수를 계산하면 컴포넌트 개수는 $15$개가 나온다. 답은 $3^15 = 14348907$이다.
8번
1번 조건은
$-2 \leq f(-2) \leq 0$
$-1 \leq f(-1) \leq 0$
$-1 \leq f(0) \leq 1$
$0 \leq f(1) \leq 1$
$0 \leq f(2) \leq 2$
로 쪼갤 수 있다. 저 조건 하에서 2번 조건을 만족하는 $f(-2), f(0), f(2)$ 쌍은 naive하게 세면 7개가 나온다. 답은 $7 \times 2^2 = 28$이다.
9번
앞 페이지에서 제일 쉬운 기하인 것 같다. 그냥 잘 그리면 $Q, M, P, D$가 일직선이다. 증명은 닮음 쓰면 된다. 나머지는 및변 길이비로 열심히 비비면 된다.
답은 500이다.
10번
유우명한 공식을 알면 쉽게 풀 수 있다. 사실 안 유명하다. PS러들한테만 유명한 것 같다. 사실 몰라도 쉽게 풀 수 있는 것 같다.
$ a^{\phi(n)} \equiv a^{\phi(2n)} (mod n)$
$36$의 배수를 $4$의배수 + $9$의배수 조건으로 쪼개자.
지금 할 풀이는 위 공식을 사용하지 않는다.
- 만약 $a, b$둘 다 $2$의 배수라면
그냥 자명하게 $4$의 배수가 된다. - $a$만 $2$의 배수라면
$a^36$은 당연히 $4$의 배수고, 나머지 두 항은 $4$와 서로소이므로 오일러 정리에 의해 각각 $1, -1$이 되어 전체가 $4$의 배수가 된다. - 둘 다 아니라면, 오일러 정리에 의해 $1 - 1 - 1$이 되어 망한다.
결론은 $a, b$ 중 적어도 하나가 $2$의 배수면 된다.
같은 논증으로 $a, b$중 적어도 하나가 $3$의 배수면 된다.
저런 쌍 개수 세주면 된다. 포배 쓰면 답은 $540$이다.
11번
이거 어케품? 일단 내가 접근한 걸 찌그려보자면
일단 $\frac{x-y}{y-z} = \frac{x-z}{y-z} - 1$로 바꾸고, 전체 식에서 $1$을 빼자. 그리고 통분하면
$\frac{x^2z - xz^2 + y - z}{xz(y-z)}$
가 된다. 여기서 가비의 리를 사용하면 어라 안되네. 분자합이 0이 되는 줄 알았는데 안 되는군.
어케품? 아마 난 $20$으로 찍었다.
12번
그냥 헷갈려서 멍충이처럼 functional graph에서 사이클이 $1, 3$사이클만 존재하는 경우만 세는 건줄 알았다. 케이스 6개 나눠서 뻘짓했다. 답은 그냥 $3$ 사이클이 존재하지 않는 것이 필충이라, $4^4 - 4\times2\times3 = 232$ 이다. 난 뻘짓해서 답이 $145$가 나왔다.
13번
근축이라 쓰고 정수론이라 읽는다. 근축이 뭔지 알면 쉽게 풀 수 있다. $O_1, O_2$근축과 $O_2, O_3$ 근축이 일치해야 하므로, 원의 방정식으로 간단히 식을 쓰면 $3p + 2q = 125$가 나온다. 이를 만족하는 정수쌍은 $21$개 있다. 답은 $21$. 근데 근축 몰라도 풀 수 있을 것 같긴 하다. 근데 좀 비자명할듯.
+ 추신, 답이 $21$이 아닌데, 세 원이 만나면 안 되는 조건에 의해 $NMK$개의 해가 빠진다고 한다.
14번
아마 답은 $13$이다. 대충 $13$인가 이상 소수부터는 쓰레기라는 것 같다. 나는 그냥 믿고 계산했는데, 누가 증명한 것 같다. 나머지는 차력쇼로 계산하면 되는데, 난 $9$개밖에 못 찾았다. 사실 그냥 이 문제 마지막에 급하게 푸느라 귀찮아서 엄밀하게 안 셌다.
$2$
$6$
$2 \times 5 \times 7 \times 11 \times 3^{1, 2, 3, 4}$
$5 \times 7 \times 11 \times 3^{1, 2, 3}$
이것만 하면 딱 $9$개이다. $13$개는 어떤애가 파이썬 돌려서 검증했다고 한다. 물론 많이 큰 수가 있으면 모르겠지만.
15번
일단 그냥 잘 모르겠어서, 찍었다. $128$차 방정식을 세운다고 생각하고 모든 근이 다 다르고 실근이라는 엄청난 개쩌는 가정을 퉁쳐서 $128$개로 찍었다. ㅋㅋㅋㅋㅋㅋㅋ 대부분은 이걸로 찍은 것 같다.
16번
5번보다 쉬운 것 같다. 진짜 그냥 보자마자 풀었다. 어떤 $1 \leq i \leq 10$가 $3$개 이상의 집합에 등장한다면, 그 집합 중 $3$개의 교집합은 공집합이 아닐 것이다. 그러므로 최대 $2$개 까지만 들어갈 수 있다. 그리고 이게 필충이다. 그러므로 $16^10 = 1099511627776$이 답이다.
17번
X쉬운 문제같은데 걍 세도 틀릴 것 같고 시간이 아마 없어서 손을 안 댔다. 뭘로 찍었는지도 모른다.
18번
그냥 안 대봐서 뭔 문제인지 잘 모른다. 딱히 할 말이 없다. 아마 식 상태를 보면 쉬울 것 같기도 한데 그냥 손 대지 말자.
19번
걍 손을 안 댔는데, 나중에 지하철에서 어떤애가 geogebra로 돌렸다. 답은 $x=38$도로 딱 떨어져서 $6x = 228$이라는 것 같다.
지인중에 저걸로 적은 사람이 있는데 어떻게 푼 건지 좀 궁금하다. 걍 기하를 잘한다.
20번
ㅁㄹ? 걍 대수는 하는게 아님.
만약 어떤 GOSU가 이 글을 보게 된다면 어딜 봐서 잘 봤냐고 할 수 있겠지만, 내 작년 점수가 더 처참했기 때문에 잘 본게 맞다 ㅇㅇ...
끝나고 지인들과 버거집에 갔는데, 그때 마침 KMO가 끝나서 그런지 주문이 밀려서 40분동안 음식이 안 나왔다. 그래서 망했다. 2시까지 가야하는데 1시 40분까지 음식이 안 나와서 취소를 하고 갔다. 근데 그때 진짜 사람이 많았다. 무슨 버거를 $NMK$개를 한번에 만들고 계셨다 ㅋㅋ
체크인을 먼저 해서 명찰을 단 상태였는데, 어쩌다보니 명찰 안에 로그인 정보가 빠져있었다. 다행히도 어떻겐가 복구했다.
타임라인은 귀찮아서 안 적을 것이다.
A
아니 A를 읽었는데, 분명 제일 쉬운 문제라는데 X어려웠다. 옆사람이 지인이였는데, 스윽스윽하더니 $N$분만에 풀어버렸다. 나는 $38$분이나 걸렸다 ㅋㅋㅋㅋ.
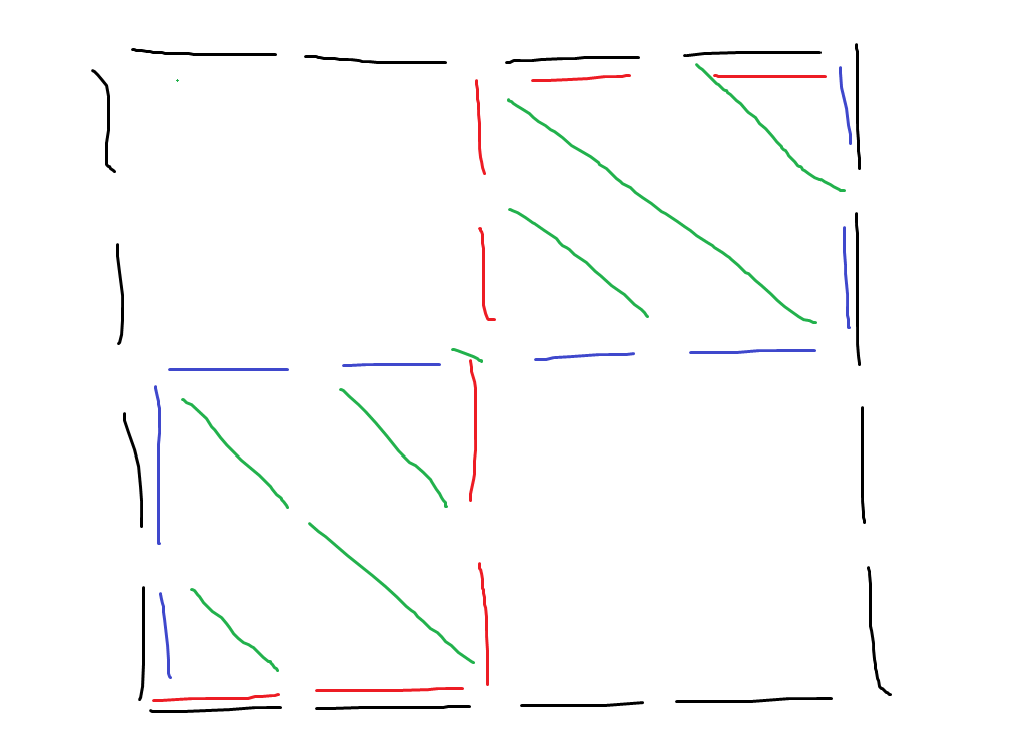
한 번 연산에 저 초록색 대각선 하나를 1 줄이거나 1 늘릴 수 있다.
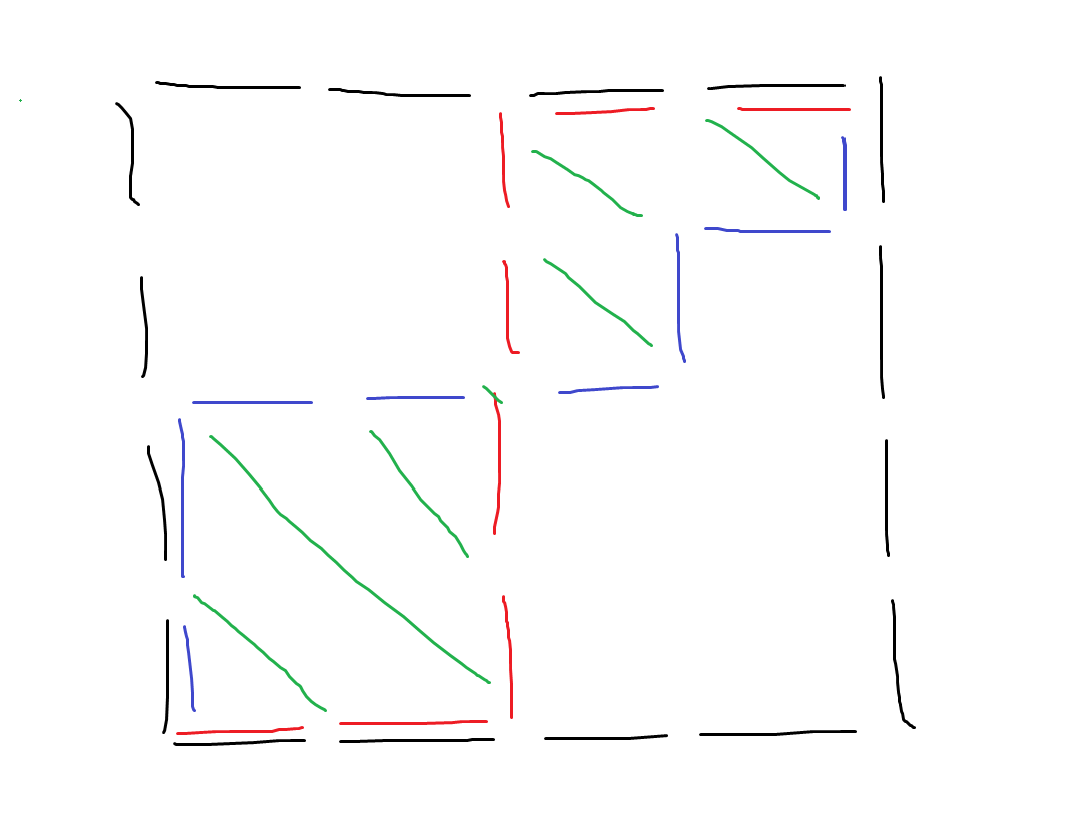
이런느낌. 그래서 각 초록색 대각선을 모두 양수로 만들거나 모두 음수로 만들면 되므로, $O(N)$에 계산할 수 있다.
근데 진짜 X어렵다. 나는 분노의 P3기여를 갈길 것이다.
B
거꾸로 보면 된다. 만약에 맨 마지막 쿼리가 불안정 정렬이라면, 각 뭉탱이마다 $(개수)!$을 곱하주면 된다.
안정 정렬이라면, 각 더미를 나눈 후 더미마다 재귀를 들어가면 된다. 각 더미의 순서로써 있을 수 있는 경우의 수의 곱 느낌이다.
근데 $3$틀정도를 박았는데, 개수를 세기 위해 카운팅소트를 했는데 배열 범위를 $3000$으로 잡았다. $A \leq 10^6$이라더라 ..
J
B를 풀고 그다음 제일 솔브가 많았던 J를 봤다. 음 쉬웠다.
매내처 마나커 마나허
근데 해싱을 막 대충 하다가 ㅋㅋㅋ TLE를 몇번 맞았다.
D
D랑 E가 솔브가 많아서 둘 다 봤는데, 일단 D는 너무 파라였다. 근데 그 다음 구성을 어떻게 할지 잘 안 떠오르는 관계로 E를 봤는데, 뭔가 식정리를 잘 하면 될 것 같았다. 근데 N번 정리해서 wolframalpha에 때려박는데 안나오더라 ㅋㅋ. wolfram이 못 풀면 인간이 정리할 수 없는 식이므로, 일단 과감하게 버렸다. 그리고 D를 다시 봤는데 흠... 하다가 ainta 이분이 너무 빨리 짜셨길래 뭐지? 막 이분그래프 만들어서 열심히 구성차력쇼를 하는게 아닌가? 라고 생각했더니, 2-sat으로 모델링을 하면 깔끔하게 뇌빼고 판정할 수 있다는 걸 알았다. 구현해 다행히 아마 한 번에 AC를 받았다.
E
다시 봤는데, 약간 문제 이해를 잘못했었다. 근데 그래도 식정리는 안되더라 음. 하다가 최근에 ARC Div1 C에서 식정리 다 해두고 못 풀어버린 경험이 생각이 났다. 그렇다. online FFT 문제였다 ㅋㅋ. 이번에 처음 짜 봤는데 구현은 쉬웠다. 사실 짜면서 아니 E부터 online FFT가 나온다고? 근데 다른 풀이는 생각이 안 나는 관계로 그냥 짰다. TLE를 받았는데, AC-library에서 스윽 긁어와서 맞았다. 그냥 내 NTT 템플릿이 느렸던 것 같다. 아 물론 출처 표기 했다. 끝나고 어떤 분 왈 online FFT가 정해인 문제를 내서 나는online FFT 를 썼을 뿐이라더라 음.
~
F가 솔브가 꽤 있었는데, 일단 읽었다. 백덤블링을 하면서 봐도 그리디인데 흠 잘 모르겠다. 빌라봉이라는 문제와 어딘가 닮아있는데 좀 다른 것 같다. 열심히 사풀이를 짜다가 틀림을 알고 현타가 왔다 ㅋㅋ.
G도 봤었는데, IOIOI Cards와 좀 닮아있었다. 음 왜 못풀었지?
H를 끝나기 30분전에 봤는데, 식정리를 했더니 식이 나왔다. 근데 남은 시간이 없어서 반쯤 짜다가 끝났다. F에 너무 시간을 쓴 것 같다.
C는 아예 솔브가 없어서 안 읽었었는데, JOI Fire ~= 인 문제였다. 근데 저걸 짤 자신은 없었으므로 안 읽길 잘한 것 같다 ㅋㅋ.

결론 : 사실 둘 다 목표에 비해 그렇게 잘 본 건 아니긴 한데 내 마음속의 기준은 만족시킨 것 같다. 기부니가 좋다.