NOI 2023 桂花树$($Osmanthus Tree$)$

문제 요약

크기가 $n$인 트리 $T$가 주어진다. 모든 노드가 "부모 노드의 번호가 자신보다 작다"는 성질을 만족한다. 이제 $n+m$개의 노드를 가진 트리 $T^{\prime}$이 몇 개나 있는지를 구하려 한다. 이때 $T^{\prime}$은 다음 두 가지 조건을 만족해야 한다.

 

• 임의의 $1 \leq i, j \leq n$에 대해, $LCA(i, j)$는 $T$와 $T^{\prime}$에서 동일하다.
• 임의의 $1 \leq i, j \leq n+m$에 대해, $T^{\prime}$에서 $LCA(i, j) \leq max(i, j) + k$이다.

 

풀이

$T^{\prime}$에서 ${1, 2, 3 \dots n}$의 위치관계는 기존 $T$와 같아야 함을 알 수 있다. 즉, 기존 $T$에서 사이사이에 적당히 노드를 끼워넣은 형태여야 한다.

 

트리 $T^{\prime}$에서 노드를 하나씩 제거하여 $T$에 도달하는 과정을 생각하자.

일단 알아둬야 할 것은, 기존 $T$의 간선 정보는 1도 필요하지 않다. 받자마자 버려도 된다.

 

$k = 0$인 경우

제일 수가 큰 노드부터 제거한다고 생각해보자. 이 노드의 자식은 "최대 하나"여야 한다. 2개 이상 있으면 조건 2에 모순이기 때문이다. 제거할 때 일종의 축약, 즉 자식이 있는 경우 자신을 삭제하고 부모와 자식을 이어준다고 생각하자. 반대로 $N+1$번 노드부터 $N+M$번 노드까지 차례대로 추가한다고 생각하면, $i$번 노드를 추가하는 형태는

• 기존에 있던 간선 사이에 내가 낌. $i-2$가지.
• 어떤 노드의 자식으로 새로 들어감. $i-1$가지.

위 2가지가 있음을 알 수 있다. 그러므로 답은 

 

$\prod_{i=n+1}^{n+m}(2i - 3)$

이 된다.

$k > 0$인 경우

조건 2에 의해, $u$의 서브트리 중에서 $u-k$미만의 정점을 포함하는 서브트리는 오직 하나뿐이다.

그 외의 자식들이 존재한다면, 그 자식들은 모두 $번호 \geq u-k$인 정점만 갖고 있을 것이다. 이런 자식들을 특별한 자식이라고 하자. 좀 더 엄밀히 말하자면, 특별한 자식이란 "메인 서브트리"를 제외하고를 얘기한다. $u$의 자식 서브트리들이 모두 $번호 \geq u-k$라고 해서 모든 자식이 특별한 자식인 것은 아니다. 제거 과정에서 제일 마지막까지 남는 서브트리가 메인 서브트리이고, 다른 서브트리들이 모두 특별한 자식이다.

 

어떤 정점 $u$가 특별한 자식이 있는 경우, 일단 $u$의 삭제를 보류하자. 그 이후 $u$를 제외한 정점들 중 큰 정점부터 같은 과정대로 삭제(축약)하다가, 마지막 특별한 자식을 삭제하게 될 것이다. 이 정점을 삭제할 때, 비로소 $u$는 "특별한 자식"이 없게 되므로 $u$를 삭제할 수 있다. 얘내 둘을 묶어서, "동시에 삭제"하는 것으로 생각할 수 있다. 그 정점을 $v$라고 할 때, $u$와 $v$는 매칭되었다고 생각하자.

 

간단한 관찰로, 각 정점은 최대 한 개의 매칭에 속할 수 있음을 알 수 있다.

 

다음은 간단한 예시이다.

 

$n = 3, m = 4, k = 3$인 경우

이 트리를 제거해 보자. 7을 제거하려 했지만, 특별한 자식, 6이 있는 관계로 보류한다. 그 이후 6을 제거하려 시도하지만, 특별한 자식인 5가 있는 관계로 보류한다. 4는 메인 서브트리이다.

 

5를 제거 시도한다. 5는 그냥 제거할 수 있다. 그러면서, 6은 메인 서브트리인 4만 남게 된다. 그러므로, 6을 제거할 수 있다. 5랑 6은 "동시에 제거"된다. 즉, 5와 6은 매칭된다. 이후 축약과정을 거쳐 아래 트리와 같이 된다.

이제 4를 제거를 시도한다. 4를 제거할 때, 7은 메인 서브트리인 3만 남게 되므로 7과 4는 매칭된다. 이후 압축하면 1-2-3만 남은 트리가 된다.

 

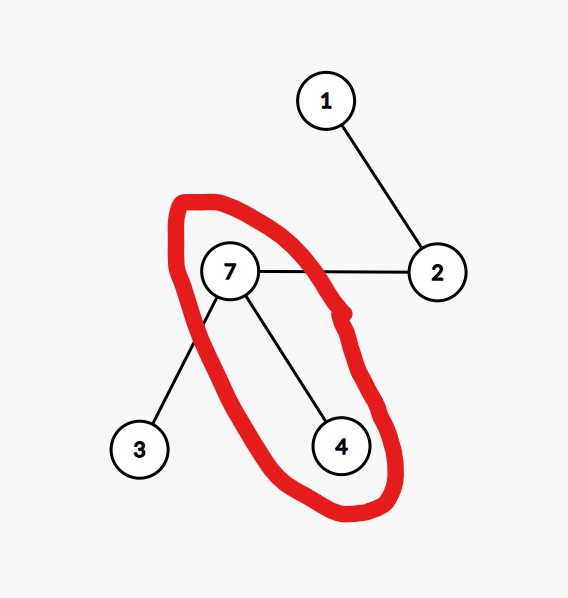
반대로 $n+1$부터 $n+m$까지 차례대로 삽입하면서, 같이 묶일 수 있는 후보군을 관리하는 bit DP를 짜면 된다.

 

DP상태를

$DP[i][S] = (n+i$번 노드를 막 추가하려는 단계에서, $[n+i, n+i+k-1]$구간 중 이미 쓴 정점들의 집합 $S)$

로 정의하자. 전이는

 

• 이미 $n+i$가 $S$에 있다면, 넘어간다.
  $DP[i+1][S \setminus {n+i}] += DP[i][S]$
• 그렇지 않으면, 다음과 같은 2가지로 나뉜다.

1. 일반 삽입:
   $DP[i+1][S] += DP[i][S] \times [2(n + i - 1 + |S|) - 1]$
2. 묶어서 삽입: $\exists v\in ([n+i-1,n+i+k]\setminus S)$
   $DP[i+1][S\cup{v}] += DP[i][S] \times (n + i - 1 + |S| - 1)$

결과적으로 최종 답은 $DP[m+1][\varnothing ]$이다. 시간복잡도는 

$O(m\times k \times 2^k)$

가 된다.

 

구현

 

후기

중국 기출은 좀 더럽거나 문제가 있을 줄 알았는데, 그 편견을 없애준 문제이다. 의외로 흠 너무 어려운데. 일단 적당히 티어를 매겼지만 솔직히 잘 모르겠다. 카운팅 너무 힘들다.