슈퍼마켓에는 각 과일에 전용 섹션이 있는 과일 코너가 있습니다. Benson이라는 토끼가 방문한 슈퍼마켓에는 $ N $ 개의 섹션과 $ N $ 개의 과일 종류가 있습니다.
섹션은 $ 1 $ 부터 $ N $ 까지 번호가 매겨져 있으며, 각 과일의 번호도 $ 1 $ 부터 $ N $ 까지 매겨져 있습니다.
- $ i $ 번째 과일의 맛 점수는 $i$ 이고, 가격은 $ C_i $ 입니다.
- $C_i \leq C_j (i< j)$ 가 보장됩니다.
각 섹션에는 고유한 과일이 배정됩니다.
- 현재 섹션 $j$에 배정된 과일의 번호는 $A_j$입니다.
- $A_j=−1$이면 해당 섹션은 비어있음을 의미합니다.
- 그렇지 않으면, $A_j$는 해당 섹션에 배정된 과일의 번호를 나타냅니다.
Benson의 행동
- Benson은 섹션을 오름차순으로 방문합니다.
- 초기에는 바구니가 비어 있습니다.
- 각 섹션에서 과일을 확인하고, 다음 조건에 따라 과일을 선택합니다:
- 바구니가 비어 있거나, 현재 섹션의 과일 맛 점수가 바구니의 모든 과일의 맛 점수보다 높을 경우, 해당 과일을 바구니에 추가합니다.
목표
슈퍼마켓은 수익을 최대화하기 위해 각 $k (1 \leq k \leq N)$에 대해 Benson이 처음 $k$개의 섹션만 방문할 때의 최대 비용 합을 계산해야 합니다.
$O(N^3)$ Solution
- $DP[i][v] = i번째 섹션까지 고려, 지금까지의 최고 맛 지수가 v일 때 최대 비용 $
과 같이 두면, $O(N)$전이를 통한 간단한 세제곱 솔루션을 얻습니다. 좀 더 자세하게는
$A_ i \neq -1$인 경우
$v = A_ i $일 때
- $DP[i][v] = C_v + DP[i-1][w] (w < A_i)$
$v > A_i$일 때
- $DP[i][v] = DP[i-1][v]$
$A_ i = -1$인 경우
$i$에서 선택한 과일이 최고 맛 점수인 경우
- $DP[i][v] = C_v + DP[i-1][w] (w < A_i)$
전에 이미 최대였던 경우
- $DP[i][v] = DP[i-1][v]$
이 두 경우의 최댓값이 $DP[i][v]$가 됩니다
$O(N^2)$ Solution
$max(DP[i][w])$값을 누적해 올라옴으로써 $O(N^2)$ 솔루션을 얻습니다.
$O(NlogN)$ Solution
모든 값이 -1이라고 생각해봅시다. $i$번째까지 봤을 때의 최댓값은 $C_N + C_{N-1} + .. C_{N-i+1}$ 일 것입니다.
그 중간에 $A_3 = 3$이라고 제한을 걸었다고 생각해봅시다. $A_3$을 먹고 오는 방법과, $A_3$을 먹지 않고 오는 방법 2가지로 나뉠 것입니다. 관찰을 해보면, $A_3$을 먹고 오는 경우와 먹고 오지 않는 게 더 좋은 경우는 "구간"으로 나타낼 수 있습니다. 즉, 적절한 구간이 존재해 $v = [x_1, x_2]$에서는 $A_3$를 먹고 오는 것이 이득이고, $v = [x_2 + 1, N]$에서는 $A_3$을 먹지 않는 것이 이득이 됩니다.
$O(NlogN)$ 솔루션은 여기서 아이디어를 얻습니다. "DP값을 구간별로 관리하는 것"
먼저, $A[i] \neq -1$인 애들 중에 절대 먹을 수 없는 애들을 전처리로 빼줍니다. 그 후
같은 기원을 가지는 $DP$값들을 모아 구간으로 관리합니다. 초기에는 $DP[0][0]$이 공통의 기원일 것이고, $A_i$를 만날 때 마다, 새로운 구간으로 분화됩니다.
구체적으로 아래 4 단계로 구성됩니다.
- 새로운 구간 생성
- 기존 비효율적인 구간 삭제
- 겹치는 구간을 제거
- 덱에 추가
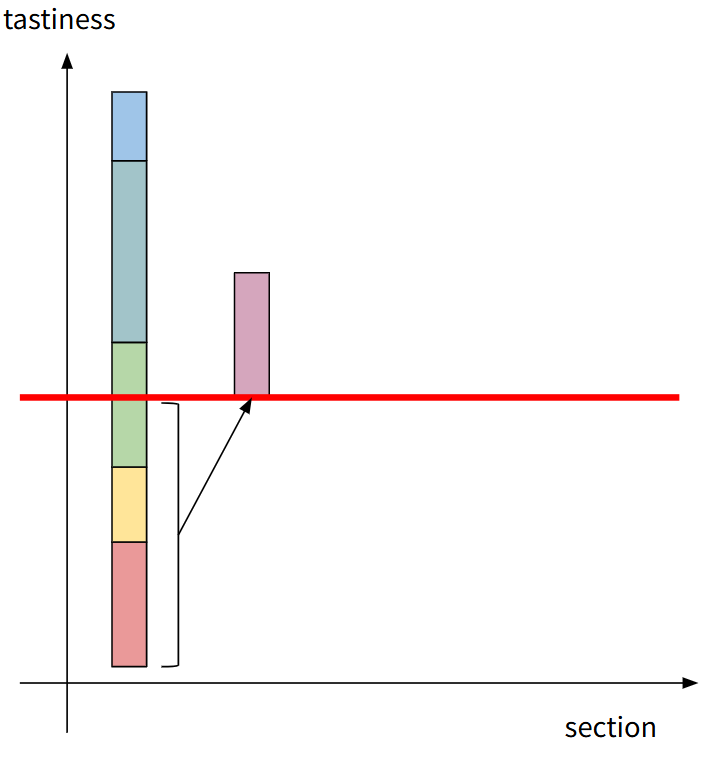

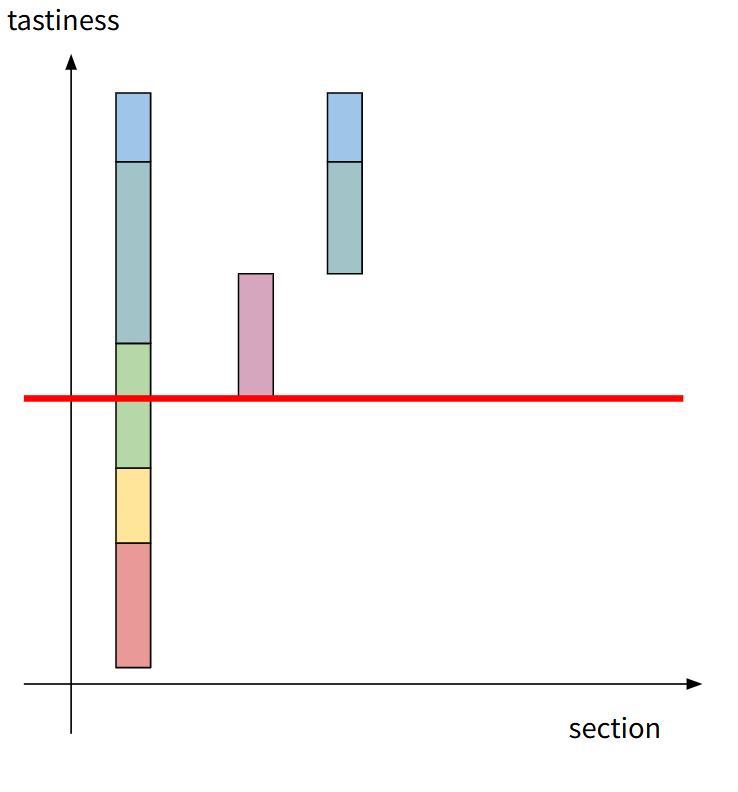
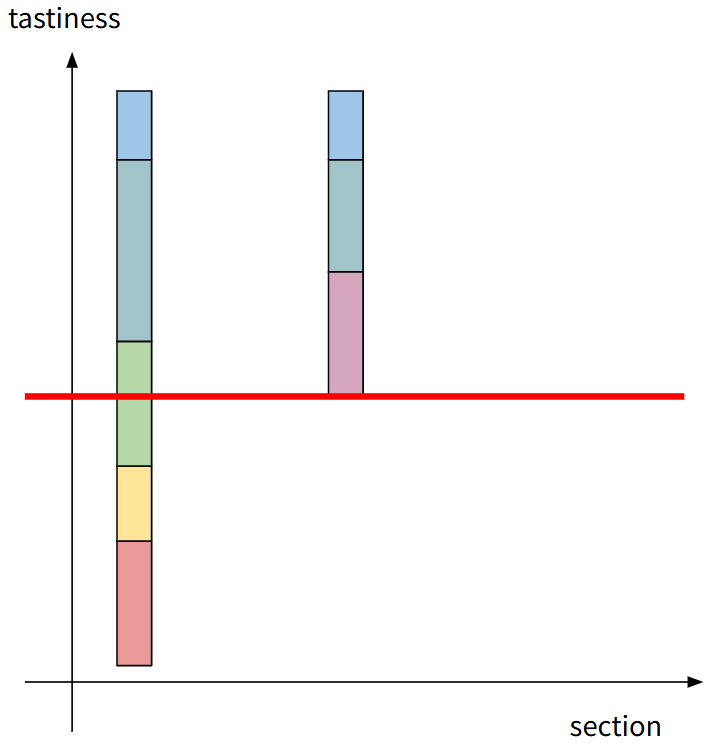
구간은 최대 1번 추가/삭제되므로 $O(N)$이 보장됩니다.
실제 최댓값은 가능한 구간 중에서 제일 위의 것을 골라 누적합을 이용해 구해줄 수 있습니다.
겹치는 구간을 제거하는 과정에서 이분 탐색을 사용하여 $O(logN)$에 위치를 찾을 수 있습니다. 총 시간복잡도는 $O(NlogN)$입니다.
'PS' 카테고리의 다른 글
| 18448 Best Subsequence (1) | 2025.01.04 |
|---|---|
| 17674 특별관광도시 (1) | 2025.01.04 |
| 10008 Polarization (3) | 2025.01.04 |
| 27355 Paths (1) | 2025.01.04 |
| 17972 Network Vulnerability (3) | 2025.01.04 |